QR 分解

阐述

设 $A$ 是 $m\times n$ 、满列秩的矩阵（ $n\le m$ ），则每一列向量是线性无关的。我们可以找到一个正交基张成同样大小的线性空间，即

\begin{cases} a_1&=r_{11}q_1\\ a_2&=r_{12}q_1+r_{22}q_2\\ a_3&=r_{13}q_1+r_{23}q_2+r_{33}q_3\\ \cdots \end{cases}

这等价于

(a_1,\cdots,a_n)=(q_1,\cdots,q_n)R; A=QR

其中 $Q$ 是 $m\times n$ 的正交矩阵，而 $R$ 是一个 $n\times n$ 的上三角矩阵。

这通常被称为「瘦」QR 分解，而「胖」QR 分解是分解为 $m\times m$ 的正交矩阵和 $m\times n$ 的上三角矩阵。

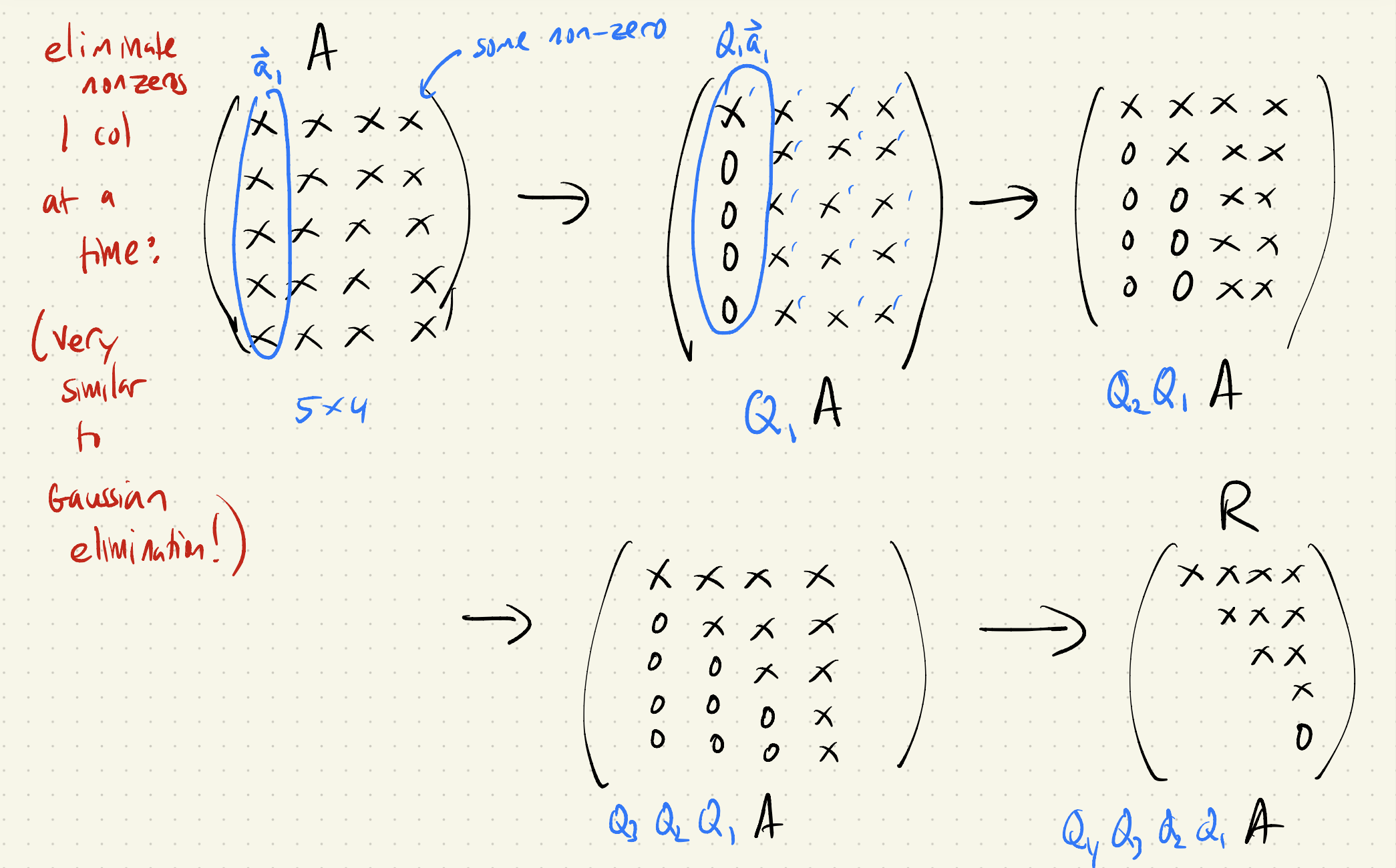
通过不断消去对角线下方的元素来转化为上三角矩阵。每一步中，

算法：

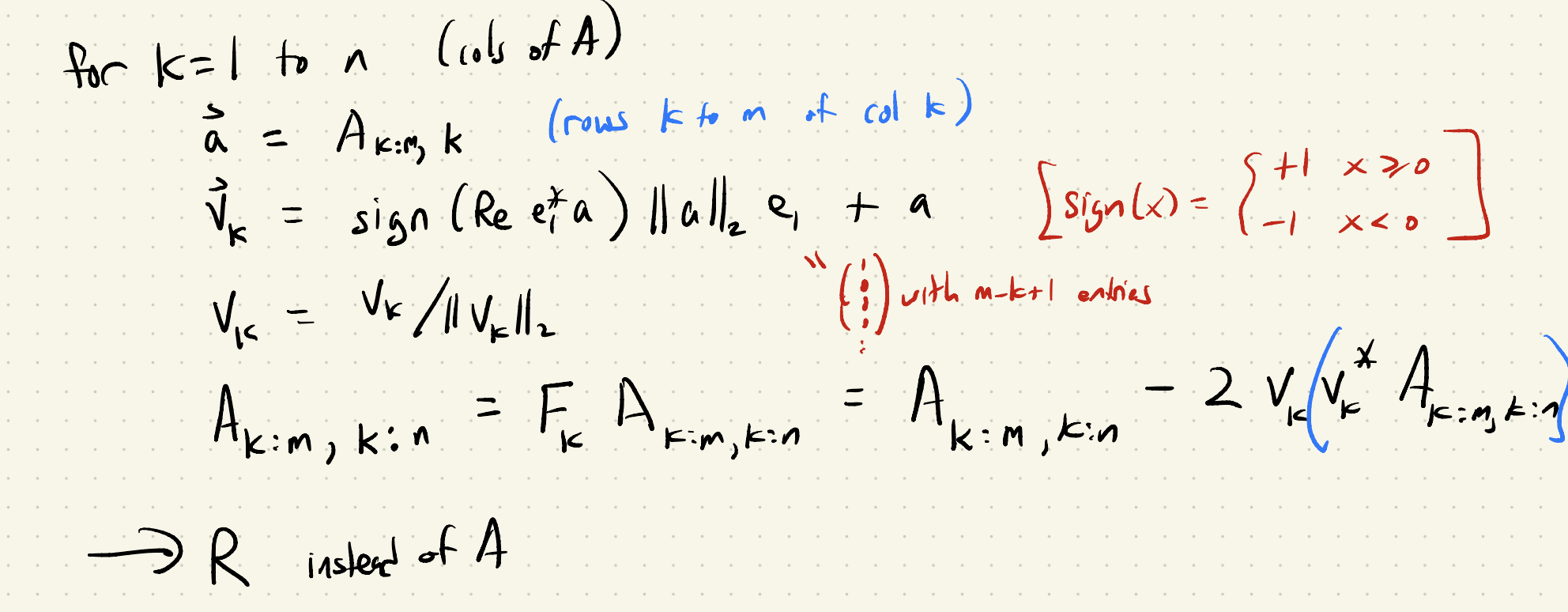
在这个过程中，我们一般不需要计算 $Q$ ，只需要存储各个向量就可以。利用这些向量，我们可以模拟 $y=Qx$ 的计算

Q=Q_1^*Q_2^*\cdots Q_n^*

所以对每个 $k=n\sim 1$ 计算 $y_{k:m}=y_{k:m}-2v_k(v_k^*y_{k:m})$ 即可。

总的 flops 为 $2mn^2-2n^3/3$ .